Regression Analysis

Linear Regression

What is linear regression?

Linear regression is a powerful and widely-used statistical model used to predict a continuous response variable based on one or more predictor variables. It is called "linear" because it assumes that the linkage between the response and predictor variables is linear.

In this tutorial, you will learn how to fit a linear regression model, interpret the results, and evaluate the model's performance.

We will also discuss some common pitfalls to avoid when using linear regression. After completing this tutorial, you can use linear regression to build predictive models to help you make data-driven decisions.

Terminology

Before we dive into the details of linear regression, it is essential to understand the basic concepts and assumptions of the model. First, let us start with the terminology:

• The response variable, also called the dependent variable, is the variable we try to predict.
• The predictor variables, also known as the independent variables, are the variables we use to make predictions.
• A sample consists of a set of observations, including a set of predictor variables and a response variable.
• A population is the set of all possible samples that could be collected.

In linear regression, we assume the relationship between the predictor and response variables is linear. The linear relationship means that the change in the response variable is directly proportional to the change in the predictor variables, holding all other variables constant. In other words, if we increase the value of one of the predictor variables by one unit, the value of the response variable will increase by a fixed amount.

In addition to the linearity assumption, linear regression also assumes that the errors (i.e., the difference between the true and value the predicted value) are normally distributed and have constant variance.

These assumptions are critical because they allow us to use statistical techniques to estimate the model parameters and make predictions.

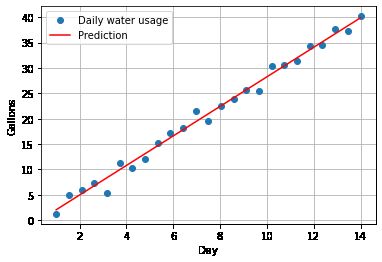
Figure 1.

Now that we have gained a fundamental understanding of linear regression concepts and assumptions, let us move on to the next step: fitting a linear regression model.

Fitting a linear regression model

There are several techniques for fitting a linear regression model, but the least squares approach is the most common. This method involves finding the model parameters that minimize the sum of the squared errors between the predicted values and the true values. In other words, we want to find the line that best fits the data by minimizing the distance between the line and the data points.

Once we have fit the model, we can use it to predict new data. To do this, we simply plug the predictor variables' values into the model equation and solve for the predicted value of the response variable.

After we have made predictions, we must evaluate the model's performance.

We can use several different metrics to evaluate the performance of a linear regression model, including mean squared error (MSE), mean absolute error (MAE), and R-squared. These metrics allow us to compare different models and choose the best performance.

In the next section, we will walk through an example of how to fit a linear regression model using least squares and evaluate its performance.

Example

To fit a linear regression model using least squares, we need to follow these steps:

• Collect a sample of data, including the predictor and response variables.
• Choose the model structure, which includes deciding how many predictor variables to include and whether to include any interaction or polynomial terms.
• Fit the model to the data by estimating the model parameters that minimize the sum of the squared errors.
• Use the model to make predictions for new data by plugging in the values of the predictor variables into the model equation and solving for the predicted value of the response variable.
• Evaluate the model's performance by calculating one or more evaluation metrics, such as MSE, MAE, or R-squared.

Let us use an example to see how these steps work in practice. Suppose we have a dataset that includes the following variables:

• \(y\): the response variable
• \(x_1\): the first predictor variable
• \(x_2\): the second predictor variable

We want to fit a linear regression model that predicts \(y\) based on \(x_1\) and \(x_2\). To do this, we will use the least squares approach to estimate the model parameters.

First, we need to choose the model structure. In this case, we will include both \(x_1\) and \(x_2\) as predictor variables, and we will not include any interaction or polynomial terms.

Next, we need to fit the model to the data. To do this, we will use an optimization algorithm to find the values of the model parameters (beta0, beta1, and beta2) that minimize the sum of the squared errors.

Once we have fit the model, we can use it to make predictions for new data by plugging in the values of \(x_1\) and \(x_2\) into the model equation and solving for the predicted value of \(y\).

Finally, we can evaluate the model's performance by calculating one or more evaluation metrics, such as MSE, MAE, or R-squared. Evaluation metrics allow us to compare the model to other models and choose the one that performs the best.

---

Linear regression is a type of analysis used in statistics. We can use it to model a linear relationship between a dependent variable, alternatively, one or more independent variables.

In a linear regression model, we usually denote the dependent as \(Y\) and the independent variable(s) as \(X\). The sole purpose of linear regression is to find the line of best fit that can, as accurately as possible, predict the value of \(Y\) given the value of \(X\).

If we minimize the sum of the squared differences between the observed Y and the lines predicted by the line, we will find the best fit. The equation

\[Y = aX + b\]

represents the line of best fit, where \(a\) and \(b\) are the determined coefficients.

The slope of the line is the coefficient and represents the change in \(Y\) for a given change in \(X\). The coefficient \(b\) is called the intercept and represents the point at which the line crosses the \(Y\)-axis.

Linear regression helps make predictions about the dependent variable given a value of the independent variable(s). For instance, if a business wants to predict the amount of revenue it will generate based on the number of units it sells, it could use linear regression to model the relationship between revenue and units sold. The company could use the model to make revenue predictions based on sales values.

Linear regression is a valuable tool for understanding and predicting the relationship between variables, but it has some limitations. One of the assumptions is that the relationship between the variables is linear, which may not always be the case. It also assumes that the variables are independent, which may not always be true.

We will look at more on the specific assumptions below. Despite these limitations, linear regression is still a widely used and powerful tool in statistical analysis.

Simple linear regression

Simple linear regression is a method in statistics, to model a linear relationship between two variables: A dependent variable (Y) and a single independent variable (X). It is called "simple" linear regression because it involves only one independent variable.

Multiple linear regression

Multiple linear regression is a statistical method used to model the linear relationship between a dependent variable and one or more independent variables. It is an extension of simple linear regression, which only considers the relationship between one independent variable and one dependent variable.

In multiple linear regression, the model is represented by an equation of the form:

\[y = b_0 + b_1x_1 + b_2x_2 + ... + b_n*x_n\]

In this equation, y is the dependent variable, \(b_0\) is the intercept term, and \(b_1, b_2, ..., b_n\) are the coefficients for the independent variables \(x_1, x_2, ..., x_n\).

To fit the model, we need to find the values for the coefficients \(b_1, b_2, ..., b_n\) that minimize the difference between the predicted values (obtained using the equation) and the actual values of the dependent variable.

or example, we can find the minimum difference using a method called least squares, which finds the coefficients, \(b_1, b_2, ..., b_n\), that minimize the sum, which is the squared differences between the predicted and actual values.

Once the model has been fit, we can use it to make predictions about the dependent variable given new values of the independent variables. We can also use the model to determine the comparative importance of each independent variable in predicting the dependent variable by examining the magnitude of the corresponding coefficient.

It is important to note that using multiple linear regression, we primarily assume a linear relationship exists between the dependent and independent variables. The linear relationship means that the change in the dependent variable is constant for a given change in each independent variable. If this assumption is not met, the model may not be accurate.

Assumptions of linear regression

A correct usage of linear regression means that we must make several assumptions about the data:

Linear relationship:

There is a linear relationship between the dependent and independent variables. This means that the change in the dependent variable is constant and predictable for a given change in the independent variables.

Independence of errors:

The errors (residuals) of the model are independent. This means that the error for one observation is not related to the error for another observation.

Homoscedasticity:

The errors are homoscedastic, meaning that the variance of the errors is constant across all levels of the independent variables.

Normality of errors:

The errors are normally distributed. This means that the distribution of the errors follows a bell curve shape.

No multicollinearity:

There is no multicollinearity among the independent variables. This means that the independent variables are not highly correlated with each other.

No autocorrelation:

There is no autocorrelation among the errors. This means that the errors for one observation are not correlated with the errors for nearby observations.

It is essential to check for these assumptions when conducting a linear regression analysis, as violating them can lead to incorrect results.

Evaluating the performance of linear regression models

We can use several metrics to assess a linear regression model's performance.

One metric commonly used to evaluate the performance of a linear regression model is mean squared error (MSE). We calculate MSE by taking the average of differences between the predicted values that the model predicted and the actual input values and then squaring the differences.

A low MSE indicates that the model predicts the dependent variable accurately, while a high MSE indicates that the model is not accurately predicting the dependent variable.

Another metric used to evaluate the performance of a linear regression model is R-squared, also known as the coefficient of determination. R-squared measures how well the model fits the data and is calculated as the proportion of the variance in the dependent variable that the model explains.

A high R-squared value indicates that the model is a good fit for the data, while a low R-squared value indicates that the model does not perform well for the data.

There are a few other metrics that we can use to assess the performance of a linear regression model, such as mean absolute error (MAE), root mean squared error (RMSE), and mean absolute percentage error (MAPE). These metrics are similar to MSE and R-squared, but they can be more interpretable in some cases, especially when working with data that is not normally distributed.

It is important to note that no single metric is best for evaluating the performance of all linear regression models. The appropriate metric will depend on the data's specific characteristics and the model's goals.

It is also often helpful to evaluate the performance of a linear regression model's performance using multiple metrics to get a complete understanding of how well the model is performing.

References and further reading

Rencher, Alvin C.; Christensen, William F. (2012), "Chapter 10, Multivariate regression - Section 10.1, Introduction", Methods of Multivariate Analysis, Wiley Series in Probability and Statistics, vol. 709 (3rd ed.), John Wiley & Sons, p. 19, ISBN 9781118391679.

HILARY L. SEAL, Studies in the History of Probability and Statistics. XV The historical development of the Gauss linear model, Biometrika, Volume 54, Issue 1-2, June 1967, Pages 1-24, DOI: 10.1093/biomet/54.1-2.1

Tibshirani, R. (1996). Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society. Series B (Methodological), 58(1), 267-288. 2346178.

Gelman, A. (2007). Book Review: Berk, R. (2004). Regression Analysis: A Constructive Critique. Thousand Oaks, CA: Sage. 259 pp. Criminal Justice Review, 32(3), 301-302. DOI: 10.1177/0734016807304871.

Tsao, M. Group least squares regression for linear models with strongly correlated predictor variables. Ann Inst Stat Math (2022). DOI: 10.1007/s10463-022-00841-7.

Hidalgo B, Goodman M. Multivariate or multivariable regression? Am J Public Health. 2013 Jan;103(1):39-40. doi: 10.2105/AJPH.2012.300897. Epub 2012 Nov 15. PMID: 23153131; PMCID: PMC3518362.

Karran JC, Moodie EE, Wallace MP. Statistical method use in public health research. Scand J Public Health. 2015 Nov;43(7):776-82. doi: 10.1177/1403494815592735. Epub 2015 Jul 10. PMID: 26163023.

Ottenbacher KJ, Ottenbacher HR, Tooth L, Ostir GV. A review of two journals found that articles using multivariable logistic regression frequently did not report commonly recommended assumptions. J Clin Epidemiol. 2004 Nov;57(11):1147-52. doi: 10.1016/j.jclinepi.2003.05.003. PMID: 15567630.

Liang KY, Zeger SL. Regression analysis for correlated data. Annu Rev Public Health. 1993;14:43-68. doi: 10.1146/annurev.pu.14.050193.000355. PMID: 8323597.

Real J, Forné C, Roso-Llorach A, Martínez-Sánchez JM. Quality Reporting of Multivariable Regression Models in Observational Studies: Review of a Representative Sample of Articles Published in Biomedical Journals. Medicine (Baltimore). 2016 May;95(20):e3653. doi: 10.1097/MD.0000000000003653. PMID: 27196467; PMCID: PMC4902409.

Tetrault JM, Sauler M, Wells CK, Concato J. Reporting of multivariable methods in the medical literature. J Investig Med. 2008 Oct;56(7):954-7. DOI: 10.2310/JIM.0b013e31818914ff. PMID: 18797413.

Narula, S. C., & Wellington, J. F. (1982). The Minimum Sum of Absolute Errors Regression: A State of the Art Survey. International Statistical Review / Revue Internationale de Statistique, 50(3), 317-326. DOI: 10.2307/1402501.

"Linear Regression (Machine Learning)" (PDF). cs2750-Spring03, University of Pittsburgh.